时间序列（Time Series）和图像（Image）之间的相互转换

Posted on 2024-06-03 Edited on 2024-12-07 In Algorithm

将时间序列（Time Series）数据转换为二维图像（Image）可以显著地扩展可用的分析方法范围。

1 格拉姆角场（Gramian Angular Field）

1.1 格拉姆矩阵变换

格拉姆角场（Gramian Angular Field，GAF）是结合坐标变换和格拉姆矩阵的相关知识，实现将时间序列变换成图像的一种编码方法。格拉姆矩阵是两两向量的内积组成，可以保存时间序列的时间依赖性，却不能有效的区分价值信息和高斯噪声。因此，在进行格拉姆矩阵变换之前，时间序列需要进行空间变换，普遍的方法是将笛卡尔坐标系转换成极坐标系（半径、角度）。

对于时间序列 $X=<x_t>, t\in\mathbb N$，可通过以下步骤得到 GAF 图：

1.1.1 时间序列归一化

通过最大-最小归一化（Min-Max Scaler），将原始时间序列数据缩放到 $[-1,1]$ 或 $[0,1]$： \[ \begin{equation} \label{eq1} \tilde{x}_{-1}^{i}={(x_i-max(X))+(x_i-min(X))\over max(X)-min(X)} \end{equation} \] 或 \[ \begin{equation} \label{eq2} \tilde{x}_{0}^{i}={(x_i-min(X))\over max(X)-min(X)} \end{equation} \]

1.1.2 极坐标变换

将归一化后的数据变换为极坐标： \[ \begin{align} \label{eq3} \left\{ \begin{array}{l} \phi_i=arccos(\tilde{x}_i)&, -1≤\tilde{x}_i≤1, \tilde{x}_i\in\tilde{X} \\ r_i={t_i\over N}&, t_i\in\mathbb{N} \\ \end{array} \right. \end{align} \]

1.1.3 自定义内积

利用和角关系和差角关系，得到对应的 GASF 图和 GADF 图 \[ \begin{equation} \label{eq4} GASF=[cos(\phi_i+\phi_j)]=\tilde{X^{'}}\cdot\tilde{X}-\sqrt{I-\tilde{X^{'2}}}\cdot\sqrt{I-\tilde{X^{2}}} \end{equation} \]

\[ \begin{equation} \label{eq5} GADF=[sin(\phi_i-\phi_j)]=\sqrt{I-\tilde{X^{'2}}}\cdot\tilde{X}-\tilde{X^{'}}\cdot\sqrt{I-\tilde{X^{2}}} \end{equation} \]

1.2 格拉姆矩阵逆变换

若在归一化时对时间序列进行 0-1 归一化，则可对 GASF 通过逆变换得到唯一的时间序列。

在格拉姆矩阵变换中，GASF 图对角线上的元素与时间序列对应位置元素的平方唯一相关： \[ \begin{equation} \label{eq6} GASF_{i,i}=2X_i^2-1 \end{equation} \] 因此仅当对时间序列进行 0-1 归一化，即 $X_i \in [0,1]$ 时，可根据 GASF 对角线上的元素求得唯一的$X_i$： \[ \begin{equation} \label{eq7} X_i=\sqrt{ {GASF_{i,i}-1} \over 2 } \end{equation} \]

1.3 GAF 的 Python 示例

在 Google Colab 运行代码或下载 Jupyter Notebook。

生成时间序列数据。

# Generate time series data
t = np.linspace(0, 10, 1000)
y = 5 * np.sin(np.pi * t)

# Plot time series data
plt.figure(figsize=(10, 6))
plt.plot(t, y)
plt.xlabel('t', fontsize=14)
plt.ylabel('y', fontsize=14)
plt.title('Original Time series', fontsize=20)
plt.savefig('GAF-Original-TS.png', dpi=100, bbox_inches='tight')
plt.show()

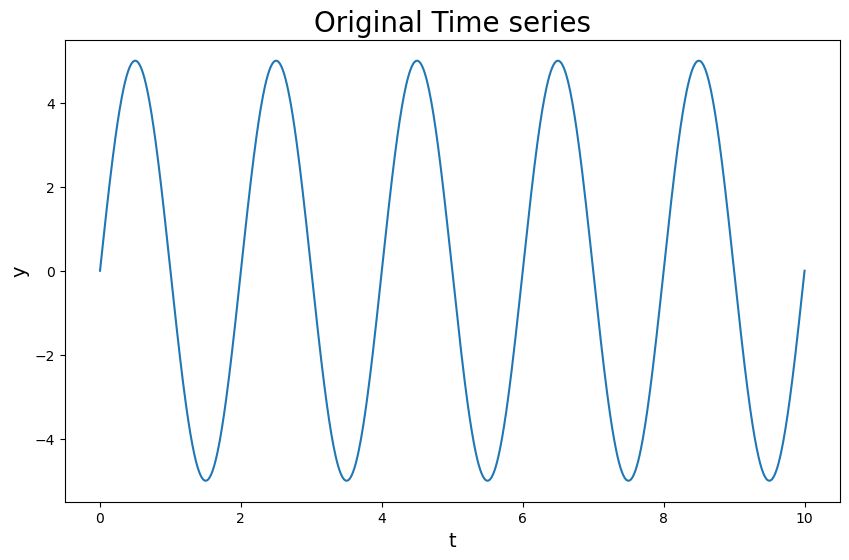
时间序列归一化。

# MinMaxScaler to [0, 1]
scaler = MinMaxScaler()
y_scaled = scaler.fit_transform(y.reshape(-1, 1))
plt.figure(figsize=(10, 6))
plt.plot(t, y_scaled)
plt.xlabel('t', fontsize=14)
plt.ylabel('y_scaled', fontsize=14)
plt.title('MinMax Scaled Time Series', fontsize=20)
plt.savefig('GAF-MinMaxScaled-TS.png', dpi=100, bbox_inches='tight')
plt.show()

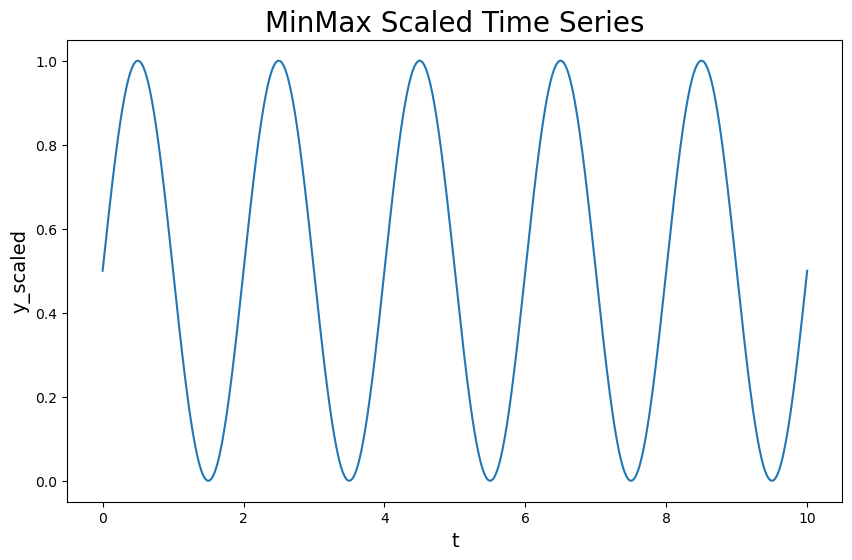
时间序列转换为 GASF。

# Time series -> GASF
gasf_size = 1000
gasf = GramianAngularField(image_size=gasf_size, method='summation', sample_range=(0, 1))
y_gasf = gasf.fit_transform(y_scaled.reshape(1,-1)).reshape(gasf_size, gasf_size)
plt.figure()
plt.imshow(y_gasf)
plt.title('GASF', fontsize=20)
plt.savefig('GAF-GASF.png', dpi=100, bbox_inches='tight')
plt.show()

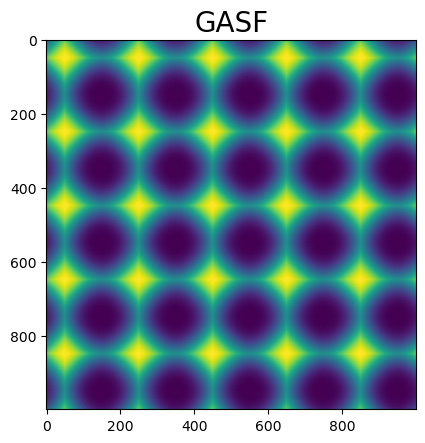
时间序列转换为 GADF。

# Time series -> GADF
gadf_size = 1000
gadf = GramianAngularField(image_size=gasf_size, method='difference', sample_range=(0, 1))
y_gadf = gadf.fit_transform(y_scaled.reshape(1,-1)).reshape(gadf_size, gadf_size)
plt.figure()
plt.imshow(y_gadf)
plt.title('GADF', fontsize=20)
plt.savefig('GAF-GADF.png', dpi=100, bbox_inches='tight')
plt.show()

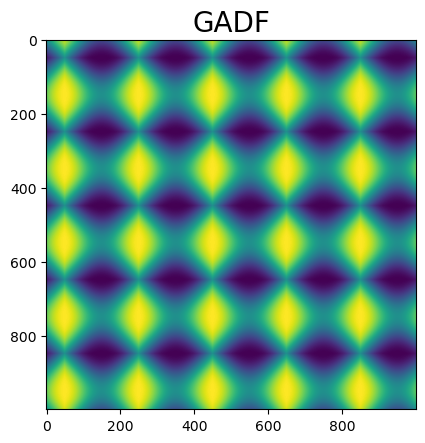
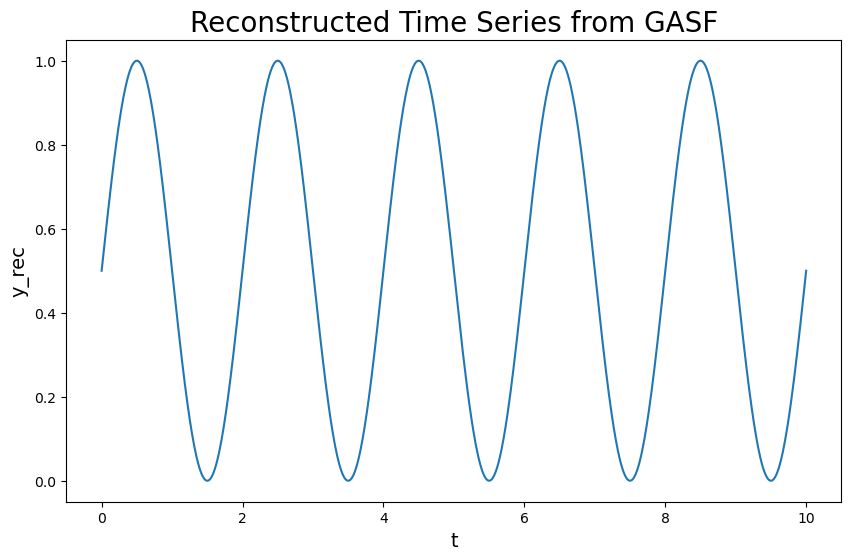
GASF 转换为时间序列。

# GASF -> Time series
def gasf_rec(data_gasf):
    data_gasf_rec = np.array([data_gasf[i, i] for i in range(gasf_size)])
    data_gasf_rec = np.sqrt((data_gasf_rec + 1) / 2)
    return data_gasf_rec
y_rec = gasf_rec(y_gasf)
plt.figure(figsize=(10, 6))
plt.plot(t, y_rec)
plt.xlabel('t', fontsize=14)
plt.ylabel('y_rec', fontsize=14)
plt.title('Reconstructed Time Series from GASF', fontsize=20)
plt.savefig('GAF-Reconstructed-TS.png', dpi=100, bbox_inches='tight')
plt.show()

1.4 参考资料

2 马尔可夫转移场（Markov Transition Field）

2.1 马尔可夫转移场

马尔可夫转移场（Markov Transition Field，MTF）是基于马尔可夫转移矩阵的一种时间序列图像编码方法。该方法将时间序列的时间推移看成是一个马尔可夫过程，即：在已知目前状态的条件下，它未来的演变不依赖于它以往的演变，由此构造马尔可夫转移矩阵，进而拓展为马尔可夫转移场，实现图像编码。

对于时间序列 $X=<x_t>, t\in\mathbb N$，可通过以下步骤得到MTF图：

2.1.1 时间序列分箱

将时间序列按照取值划分为 $Q$ 个分位箱（Bin），且每个分位箱内的数据量相同；任一数据点 $x_i$ 属于唯一的分箱 $q_j, j \in [1,Q]$。

2.1.2 构造马尔可夫转移矩阵

通过在时间轴上以一阶马尔可夫链的方式统计分位箱之间的转移频率，得到尺寸为 $[Q, Q]$ 的加权邻接矩阵 $W$，其中 $w_{ij}$ 为分位箱 $q_i$ 转移到 $q_j$ 的频率；再通过 $\sum_{j}{w_{ij}}=1$ 归一化后，即可得到马尔可夫转移矩阵： \[ \begin{equation} \label{eq8} W= \left[ \begin{matrix} w_{11} & \cdots & w_{iQ} \\ w_{21} & \cdots & w_{2Q} \\ \vdots & \ddots & \vdots \\ w_{Q1} & \cdots & w_{QQ} \\ \end{matrix} \right] ,s.t.\sum_{j}{w_{ij}}=1 \end{equation} \]

2.1.3 构造马尔可夫转移场

计算从 $i$ 时刻到 $j$ 时刻（此处 $i$、$j$ 为时间轴）时间序列的值从 $q_i$ 分箱转移到 $q_j$ 分箱的概率，记为 $M_{ij}$，即可得到马尔可夫转移场：

$$ \begin{equation} \label{eq9} M= \left[ \begin{matrix} w_{ij}|_{{x_1}\in{q_i},{x_1}\in{q_j}} & \cdots & w_{ij}|_{{x_1}\in{q_i},{x_n}\in{q_j}} \\ w_{ij}|_{{x_2}\in{q_i},{x_1}\in{q_j}} & \cdots & w_{ij}|_{{x_2}\in{q_i},{x_n}\in{q_j}} \\ \vdots & \ddots & \vdots \\ w_{ij}|_{{x_n}\in{q_i},{x_1}\in{q_j}} & \cdots & w_{ij}|_{{x_n}\in{q_i},{x_n}\in{q_j}} \\ \end{matrix} \right] \end{equation} $$